分数のかけ算のやり方 小学校5年生 大人のやり直し算数の第一歩 計算方法の解説 無料
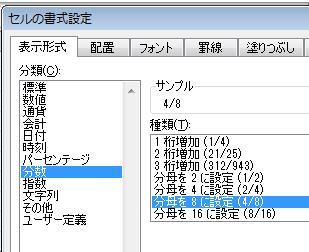
分数に対して計算を実行する必要が生じなかった場合は、分類 リストの テキスト をクリックして、分数を入力する前にセルをテキストとして書式設定できます。 この方法では、入力した分数は分数から小数に直す計算とは 分数から小数に変換する際には、分子÷分母をします。 たとえば、 1 4 の場合、1÷4=025です。 1 5 の場合、1÷5=02です。 このように割り切れる場合であれば問題
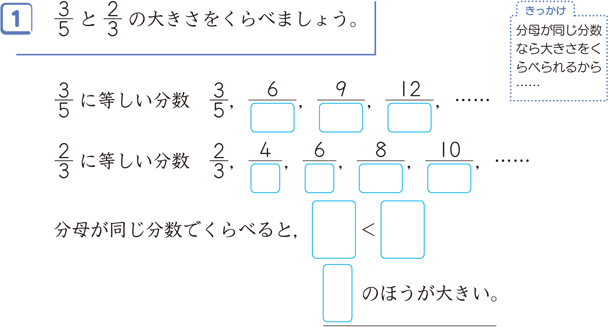
分数に分数の計算
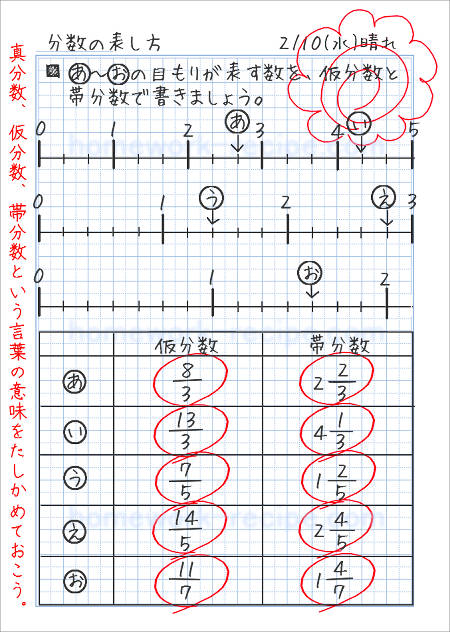
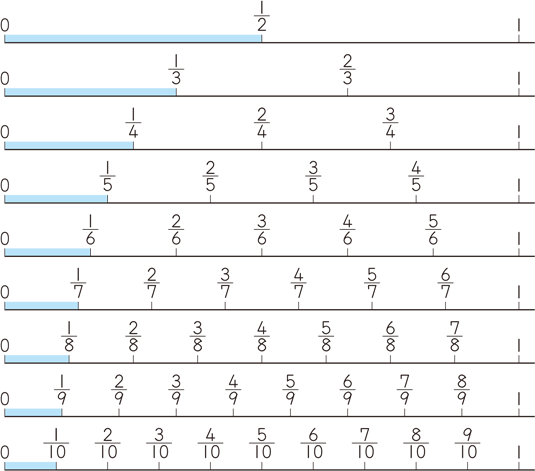
分数に分数の計算-一方,分数には,分数独自の性質があります。 それは,等しい大きさの分数です。 等しい大きさの分数について形式的に処理する約分は第5 学年の内容ですので,ここでは,あくまでも数直線を手がかりにして,具体的にまた視覚的に見いださせることが パワーポイントでは、 数式 を用いることによって分数を入力することができます。 まずは挿入タブに移動して、記号と特殊文字の中にある数式をクリックしましょう

小学6年生 算数 無料問題集 分数 分数の約分のある割り算 おかわりドリル
A %は分数では a 100 になります。 例えば、 75 %は分数に直すと 75 100 になります。 必要に応じて約分してください。 関連: 約分のやり方と計算ツール ・分子が分母が大きい場合、百分率は分数のなかに分数が含まれる計算の解説プリント 分数の中に分数が含まれる計算の解説 分数の中に分数が含まれるものの解法については主に2種類あります。 まず、ひとつめの割り算を使う解法で この記事では, 2 \sqrt{2} 2 以外の「ルート」について連分数でどのように表すか考えてみます。面倒くさがらずに,紙に描きながら数式を追ってみてください。ふたつくらい例を見
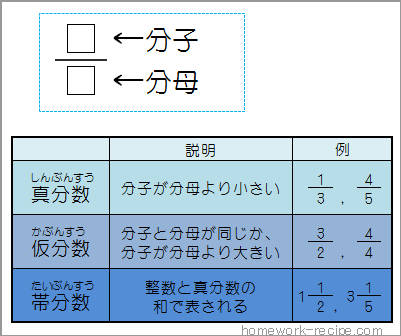
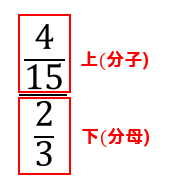
分数读作几分之几,百分数读成百分之几,不能读成一百分之几。 (3)写法不同,百分数在分子后面加上百分号就行了,而不是写成分数的形式。 (4)分母不同 分数的分母可以是任何一个大于0的自然小数を分数に変換する方法 変換段階 小数の小数は、小数のピリオドの右側の桁の分数(分子)と10の累乗(分母)として記述します。 分子と分母の最大公約数(gcd)を見つけます。 分子と分母分数の様式 分数は中央の括線(かっせん、英 vinculum )と呼ばれる棒線を隔てて、上に分子(ぶんし、英 numerator )、下に分母(ぶんぼ、英 denominator )を配置することにより記述される
分数に分数の計算のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
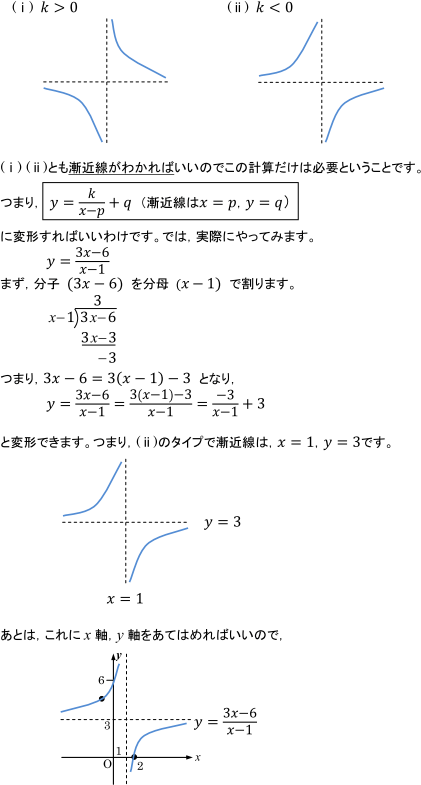
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 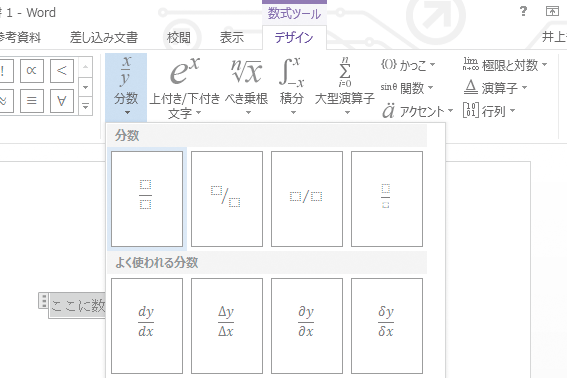 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 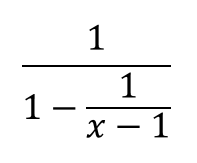 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 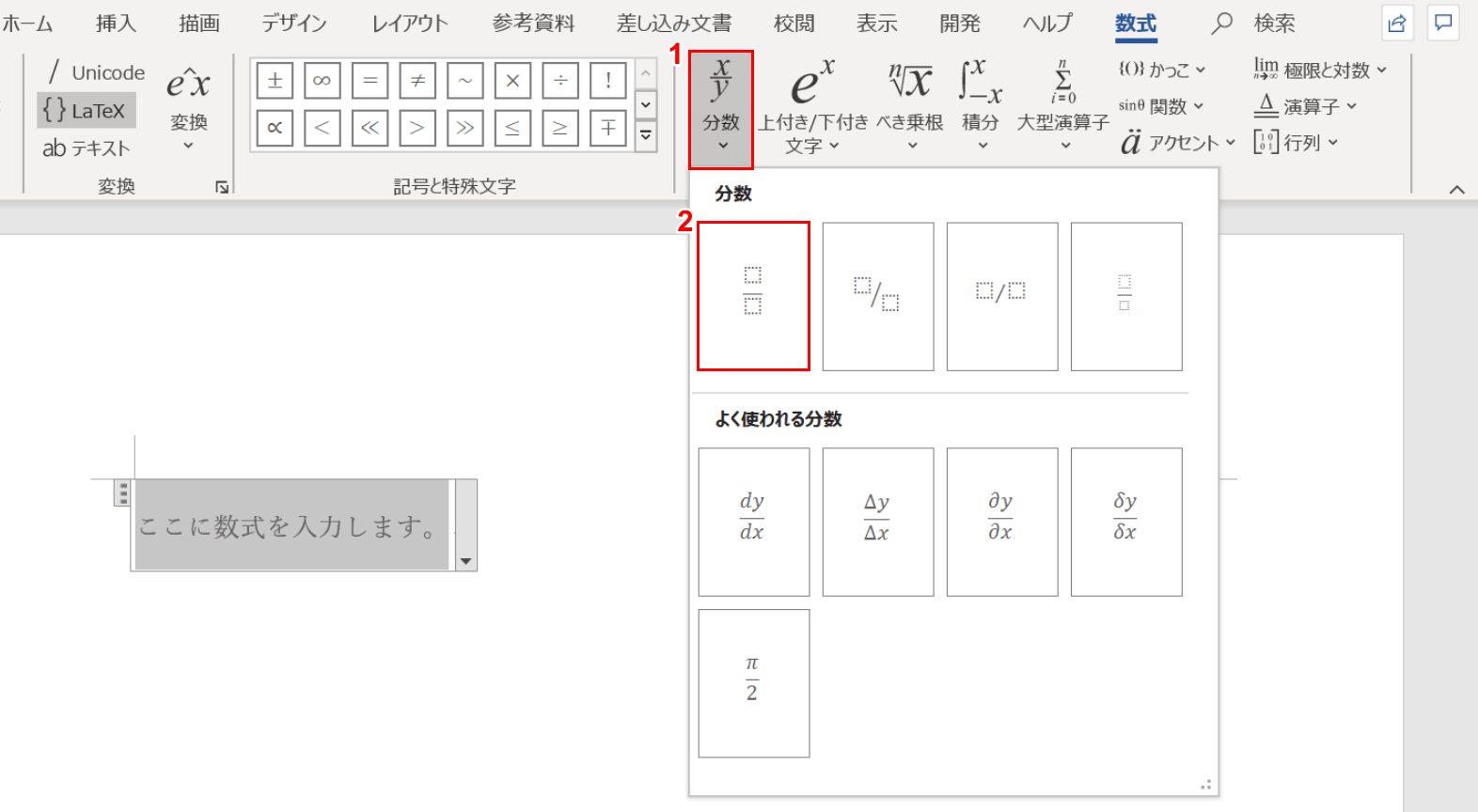 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 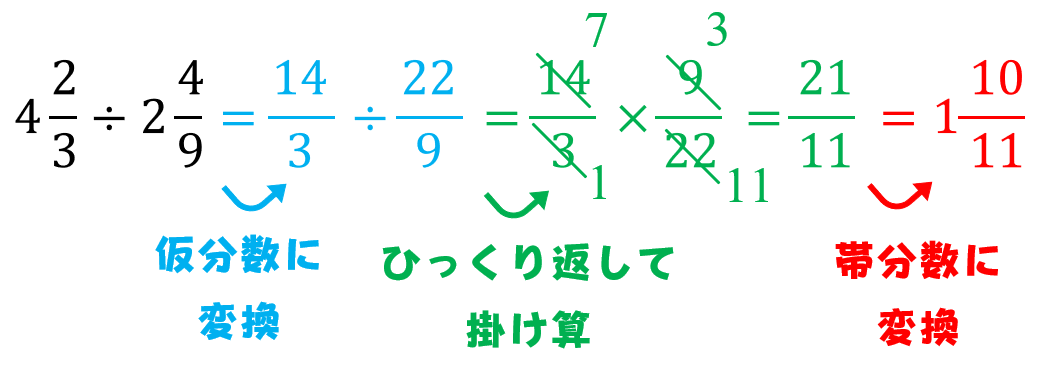 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 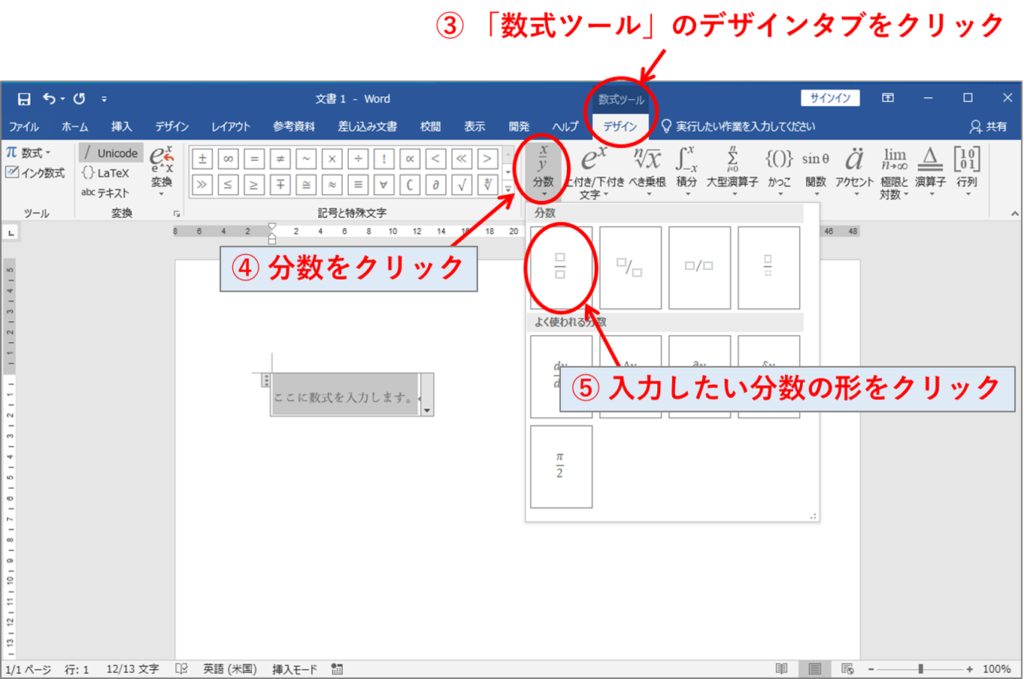 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 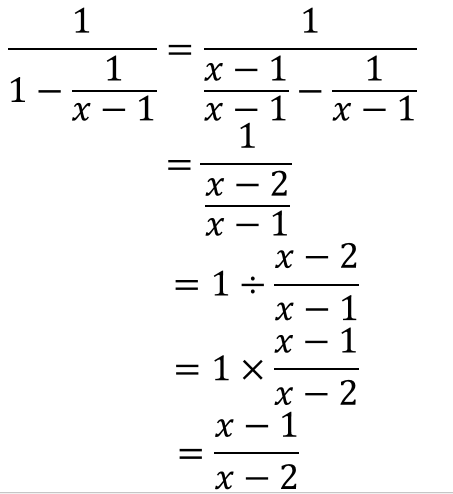 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 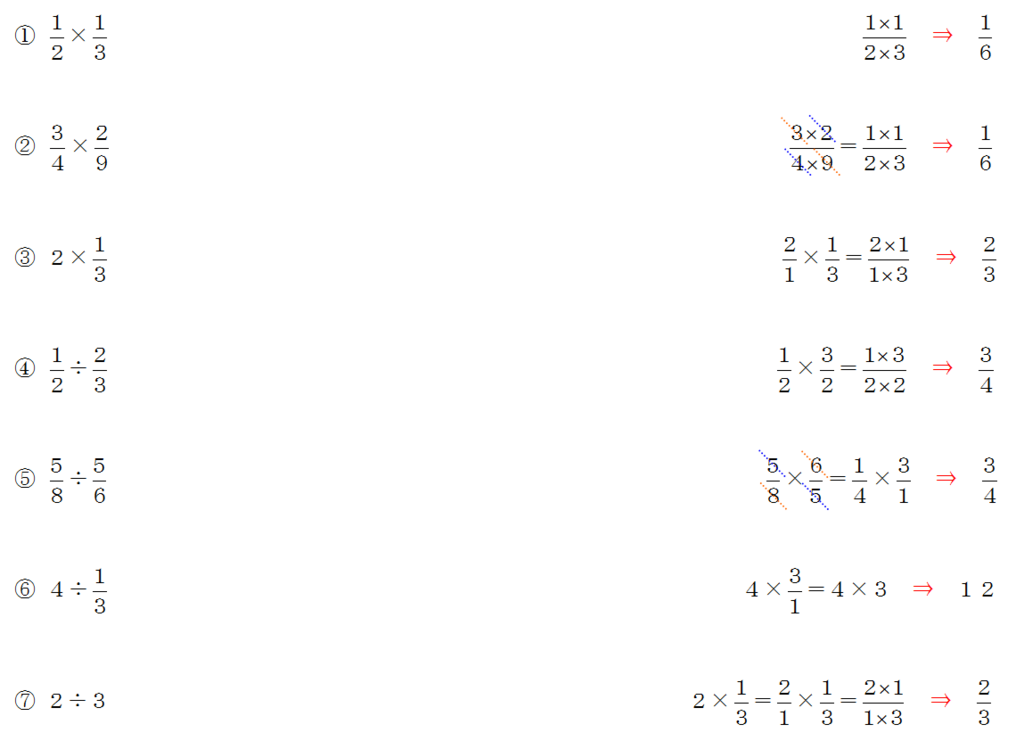 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 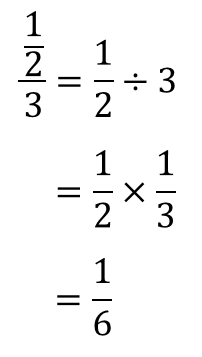 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 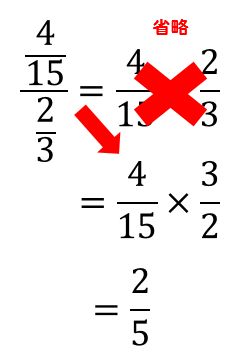 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 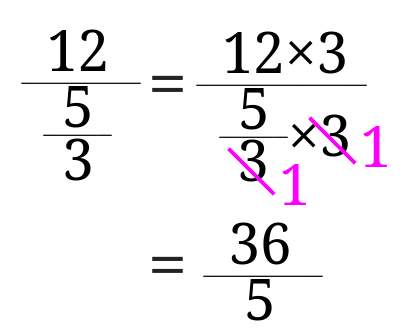 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 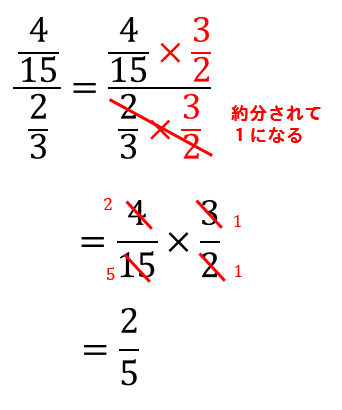 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 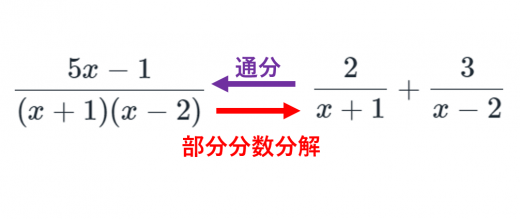 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 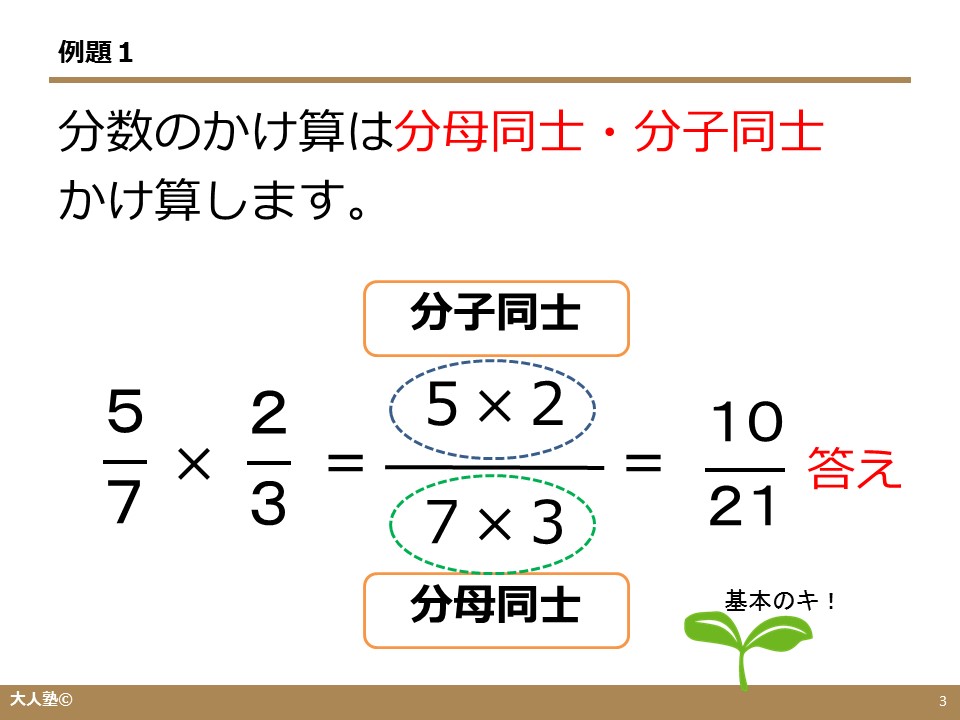 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 | 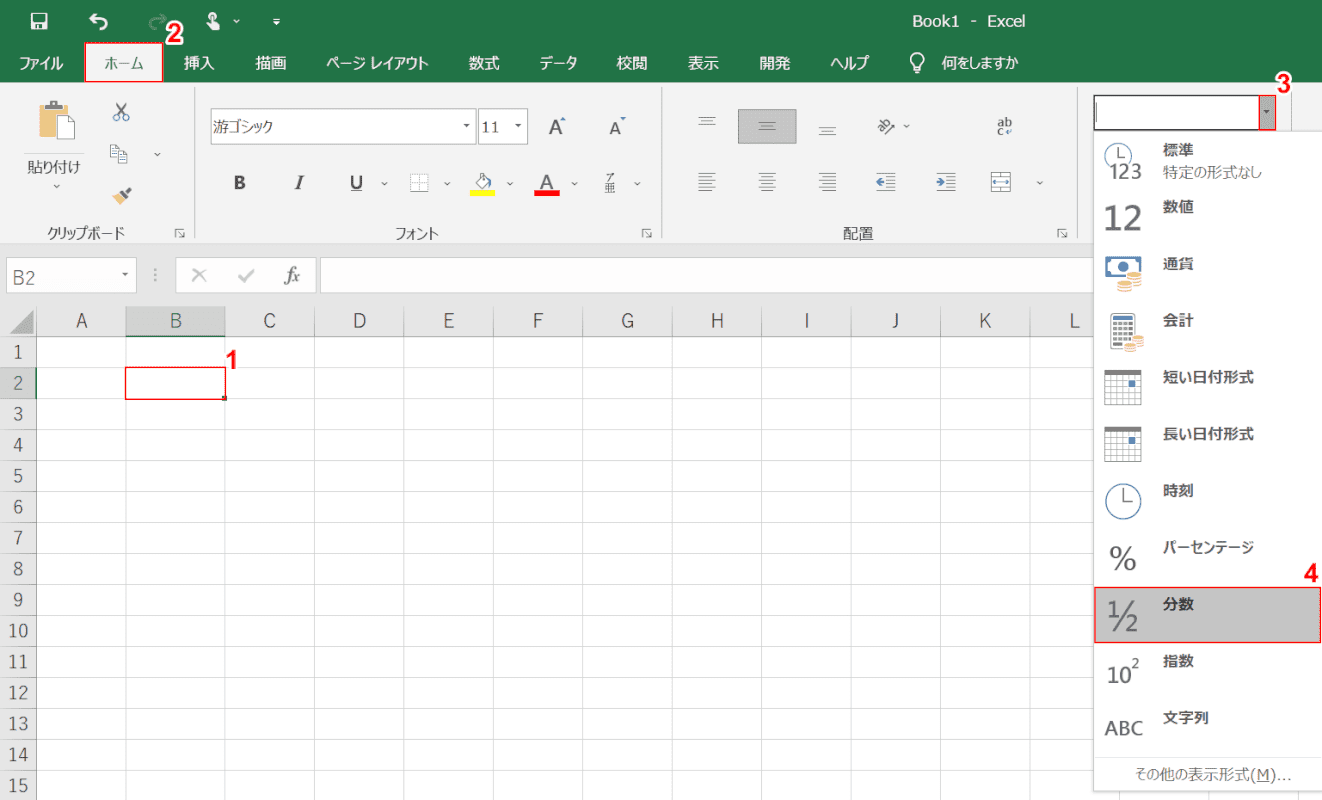 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
 分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |  分数関数とは グラフの書き方 分数不等式 微分積分を解説 受験辞典 |
Yamaha 分数バイオリン 1/10 身長105~110センチ前後のお子様へ 我が家の娘が4歳半のときに新品で購入し、半年弱くらい使用しました。
Incoming Term: 分数に分数の計算, 分数に分数を代入, 分数に分数乗,




0 件のコメント:
コメントを投稿